VIE, An Automata Sequencer

Performance and composition through metaphorical representation of living organisms

by Jingyin He, Jordan Hochenbaum and Ajay Kapur

Throughout the history of Western music, the organization of pitch and duration is often formalized by a composer’s computational thinking. Tuning systems, tonal harmony and serialism are all notable examples of computational thought processes as a means for creation. The formalization of music using cellular automata frees the composer from those systems by offering an alternative process, which can lead to discovery of new æsthetics in composition and performance (He and Kapur 2013).

Since the publication of the Game of Life in 1970, there have been many variations of the system and its integration in the field of music. An early application that uses the Game of Life is Cellular Automata Music generator (CAMUS), which determines the two intervals between three notes using the positions of “live” cells in the Game of Life (Burraston and Edmonds 2005). The Automaton VST by Audio Damage uses Life to drive modulation effects on audio signals. Other musical applications that feature the Game of Life algorithm as a pattern generator include Game of Life Sequencer Bank by Grant Muller, Newscool in Native Instruments’ Reaktor, GlitchDS, Runxt Life, sonicLife by hexler and Brian Crabtree’s Conway’s life for Monome. Unlike these previous applications of Game of Life, VIE is open sourced and allows users to alter and fine-tune parameters, and the open framework allows it to be used in multiple applications. Most importantly, VIE removes the user from using computation thought while in a creative state, whether they be composing or in a live performance situation.

Background

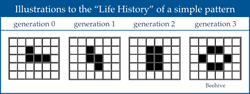
Mathematician John Horton Conway devised a two-dimensional cellular automaton 1[1. Cellular Automaton was created by John von Neumann and Stanislaw Ulam to study the process of reproduction and growth.] Game of Life in 1970. Game of Life is a simulation of the births and deaths of living organisms (Gardner 1970). In this mathematical model, cells are assigned a particular state, which then changes by turn according to specific rules that are applied according to the states of the neighbouring cells. The term “two-dimensional” refers to the movement of the cells on both the vertical and horizontal axis. The cellular automaton is based on an infinite square grid lattice in theory, but generally (and in my own work) the size of the board is defined, resulting in the number of cells presented in the arrays always being finite. The cells in the automaton have two possible states: living or dead. Traditionally, black counters are used for living cells and white counters are used for the dead (Ibid.). The eight neighbouring cells surrounding any individual cell determine the state of the individual cell in every generation.

A simple set of rules determines the state of the individual cell (Fig. 1). The automaton begins with an initial pattern. Rules of birth and death are applied throughout the array to form the next generation. These same rules are applied to the new generation that results from the initial pattern, and so on, as the pattern evolves. Figure 2 shows the life history of a simple pattern of tetrominoes, four rookwise-connected counters (Gardner 1970). At the third generation the automaton ceases. This is because the resultant pattern of the cells in the subsequent generations is constant; this pattern is called a “still life”. The automaton will cease to “exist” when any of the following conditions occur (Ibid.):

1. All the cells on the board are dead.
2. The cells settle into a stable pattern that remains unchanged in the subsequent generations.
3. The cells oscillate in a cycle of two or more periods.

Patterns in Game of Life

In Game of Life, a “pattern” is a recognizable configuration of cells that brings about deterministic behaviour in subsequent generations (Gardner 1985). Several common patterns encountered in the game can be rendered sonically, with their behaviours represented as specific patterns of sonic morphology.

A still life is a pattern of cells whose configuration settles into a stasis that has no births and deaths from one generation to the next. Commonly encountered examples of still lives are shown in Figure 3. In sound terms, their behaviour can be interpreted as a group of sound objects with a complex texture that is consistent over a period of time (Fig. 4).

Oscillators are patterns that change from an initial pattern to other patterns and back to itself over a number of generations. The “blinker” is a sonic example of a fairly simple sound pulsing between two different spectral typologies.

Spaceship configurations are patterns that translate themselves across the board over time. The simplest form of a spaceship is a configuration known as the glider. The Spaceship translating over the board can be sonified as the shifting of textures of a sound object towards a destination over time.

When a configuration is made up of fewer than 10 cells but takes more than 50 generations to stabilize, the configuration is classified as Methuselahs. Methuselah is a Biblical reference to the oldest person to have ever lived. Phrases of a meso structure or short compositions in a macro timeline can be created from Methuselah’s emergent behaviours.

VIE

Because of Life’s analogies with the rise, fall and alterations of a society of living organisms, it belongs to a growing class of what are called “simulation games” — games that resemble real-life processes (Gardner 1970).

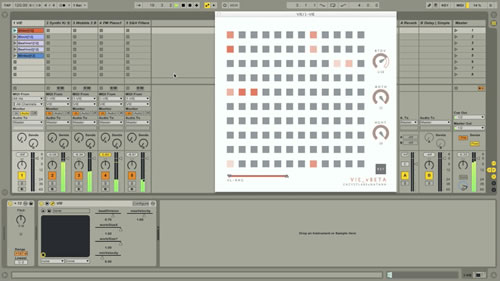
Much like the birth and death of organisms, VIE (Fig. 7) implements the Game of Life to dictate the livelihood of individual sounds. Sections or short motivic passages are created by trends and activities that occur within a single time frame. How often the generation occurs during the passage determines the duration of each passage. For instance, if a generation occurs every 10 milliseconds and there are 5 generations in that passage, the duration of the passage would be 50 milliseconds. The use of Life through VIE enables the artist to generate and dictate entire musical structures through a single implementation. Musical depth is created by patterns that constantly interact with each other during the game, as many patterns happen at once and all the patterns are affecting the others. This way, linear motivic passages, vertical textures and chronological musical sections are created through these interactions.

VIE is open source and realized in C++ programming environment, using the JUCE library. Its universal VST format encourages artists of all levels to approach performance and composition from a different perspective. Furthermore, its open-source format allows informed users to modify VIE at a lower level according to their needs for stylistically individualized applications. The main features of VIE include:

• Sync to DAW’s clock;
• Quantization of length of each generation to note duration (shortest duration at thirty-second triplet);
• Variable width and height of grid array (changeable dynamically in real time);
• Static and dynamic velocity;
• Automation for all parameters.

System Overview

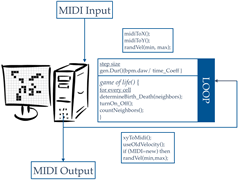
The overview of the system architecture of VIE is as shown in Figure 8. MIDI notes are formalized into the Game of Life instance as cells using an algorithm (Fig. 9). Contrary to most sequencers inspired by Game of Life that interpret the automata linearly stepping through x and/or y (such as Sequencer Bank and sonicLife), each generation of Game of Life in VIE is perceived as a step in the sequencer. This enables access to mapping options of up to 121 discrete notes in each generation. The interval between each generation, or step, is calculated using sampling rate and BPM. By default, the duration of the notes are programmed to be quantized in standard note duration from as long as a whole note to as short as a thirty-second triplet.

Each subsequent generation outputs MIDI notes by solving for m (Fig. 9). The MIDI output is then fed back into the Game of Life algorithm. Synchronously, the MIDI output can be routed to any desired sound-generating VST as MIDI messages.

At any point in time, the user is able to modify the system by inputting MIDI notes. The “RST” (reset) button removes all “live” cells present and sends note-off messages to all MIDI notes. This allows users to clear the Game of Life array and start afresh.

The velocity of each MIDI note is generated randomly within a desired range determined by the user using a two-headed slider. Constant MIDI velocity is also possible when the two headers are set in the same position. The velocity parameter of each note is reflected visually by the alpha value of each “live” cell.

Media Examples

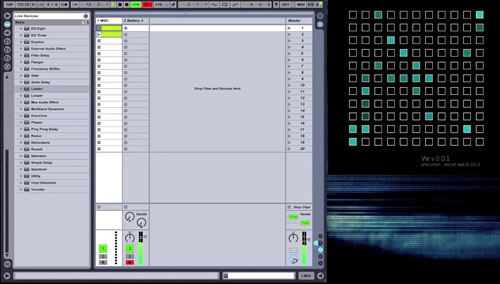
VIE can be run in Ableton Live and can be made to control various VSTs and instruments, such as Native Instruments’ drum sampler, Battery (Video 1).

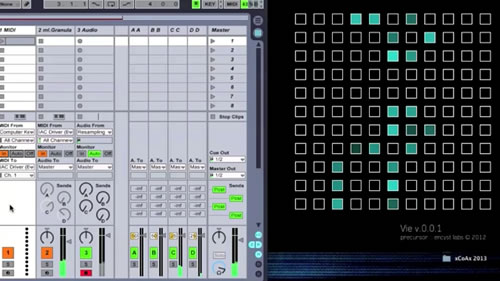
Using granular synthesis in Max for Live, VIE has been used to sample the first five seconds of Edgard Varèse’s Amériques (Video 2). The initial seed used is a variation of a Die Hard methuselah configuration, which settles into a stable pattern that remains unchanged in subsequent generations.

VIE can be used to control multiple simultaneous instruments (Video 3).

Bots Formalization is a recent research and performance project of mine that utilizes a customized version of VIE to interface the mechanical onsets of actuators to a controller that breathes the Game of Life (Video 4).

Conclusion

This article presented a tool that brings the musical application of Conway’s Game of Life to composition, and a different perspective of mapping the parameters of the cellular automata to musical parameters. Instead of the common approach of perceiving each column of the Game of Life grid as a step in time, VIE utilizes the temporality of each generation to determine the length of each passage. Consequently, this mapping strategy shapes the form of the composition. The metaphorical representation of living organisms through Conway’s Game of Life drives the organization of sonic materials to inject new characteristics into composition and performance.

Bibliography

Burraston, Dave and Ernest Edmonds. “Cellular Automata in Generative Electronic Music and Sonic Art: A Historical and technical review.” Digital Creativity 16/3 (Fall 2005), pp. 165–185.

Dennett, Daniel C. Consciousness Explained. Boston: Back Bay Books, 1992.

Dorin, Alan. “Generative Processes and the Electronic Arts.” Organised Sound 6/1 (April 2001), pp. 47–53.

Gardner, Martin. “Mathematical Games: The Fantastic combinations of John Conway’s new solitaire game ‘Life’.” Scientific American 223 (Fall 1970), pp. 120–23.

_____. “The Game of Life, Part III.” In Wheels, Life and Other Mathematical Amusements. New York: W.H. Freeman & Company, 1985.

He, Jingyin and Ajay Kapur. “Formalization Using Organic Systemization for Musical Applications.” xCoAx 2013. Proceedings of the 1st International Conference on Computation, Communication, Aesthetics and X (Bergamo, Italy: Università degli Studi di Bergamo, 27–28 June 2013). http://2013.xcoax.org

Rosenboom, David. “The Performing Brain.” Computer Music Journal 14/1 (Spring 1990) “New Performance Interfaces (1),” pp. 48–66.